Answering Numerical Questions That Check Significant Figures

Similarly, why are full-size figures no longer used in math? 12) Why are huge figures NOT critical whilst solving problems to your math class? Math lessons don't address measured values. As a end result, all of the numbers are taken into consideration to be infinitely particular.Likewise, why can we spherical to tremendous figures?

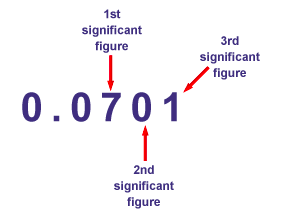
We round up due to the fact the first parent we cut off is 9. 0.0020499 to a few extensive figures is 0.00205. We do not positioned any greater zeros in to the right after the decimal factor. This is due to the fact we do now not want them to maintain the precise area cost for the widespread digits.

What is a tremendous parent in physics?

In physics issues, you use tremendous digits to express your solutions. Significant digits, additionally often known as significant figures, represent the accuracy with which you know your values. Note the variety of digits: The first cost has how to calculate significant figures 3 considerable figures, the opposite most effective two.

 What is the which means of significant digits in size?

Significant digits (also called substantial figures or “sig figs” for short) suggest the precision of a size. A range with more huge digits is more particular. For instance, eight.00 cm is greater precise than eight.0 cm.

Rules For Determining If a Number Is Significant or Not

All non-0 digits are considered sizeable. For example, 91 has  large figures (9 and 1), at the identical time as 123.Forty 5 has five amazing figures (1, 2, 3, 4, and five).Zeros performing amongst  non-zero digits (trapped zeros) are considerable. Example: one 0 one.12 has 5 large figures: 1, zero, 1, 1, and

Leading zeros (zeros before non-zero numbers) are not full-size. For instance, 0.00052 has  big figures: five and a couple of.Trailing zeros (zeros after non-0 numbers) in a range of without a decimal are commonly not big (see beneath for extra data). For example, four hundred has only one massive decide (four). The trailing zeros do no longer rely as extensive.

Trailing zeros in a variety of containing a decimal aspect are great. For instance, 12.2300 has six massive figures: 1, 2, 2, three, 0, and zero. The variety 0.000122300 nevertheless has best six tremendous figures (the zeros in advance than the 1 are not big). In addition, 120.00 has five significant figures since it has three trailing zeros. This convention clarifies the precision of such numbers. For example, if a dimension this is specific to four decimal places (zero.0001) is given as 12.23, then the dimension is probably understood as having only two decimal places of precision available. Stating the stop result as 12.2300 makes it smooth that the size is specific to four decimal places (in this example, six good sized figures).

The range 0 has one giant discern. Therefore, any zeros after the decimal thing are also large. Example: zero.00 has three huge figures.Any numbers in clinical notation are taken into consideration massive. For instance, four.300 x 10-four has 4 tremendous figures.